Transform Types¶

In openAbel due to the equispaced discretization all methods truncate the Abel transform integral, e.g. for the forward Abel transform

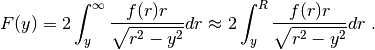
$F(y)=2\int_y^\infty\frac{f(r)r}{\sqrt{r^2-y^2}}dr\approx2\int_y^R\frac{f(r)r}{\sqrt{r^2-y^2}}dr\; .$

This is sometimes called finite Abel transform. Since 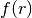$f(r)$ often has compact support or decays very quickly (and 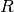$R$ can be chosen very large with a fast transform method) this introduces an arbitrarily small error.

It should be noted that often one can use variable transformations or other discretizations to simplify the calculation of the above integrals. However, often one is interested in exactly the in openAbel implemented case on equispaced discretization. This is often due to the relation of the Abel transform with the Fourier and Hankel transforms and the desire to use the same discretization as the FFT or a discrete convolution, or just by the given data (e.g. from experiments).

The type of transform can be chosen by setting the forwardBackward parameter:

import openAbel
abelObj = openAbel.Abel(nData, forwardBackward, shift, stepSize)

The parameter stepSize is the grid spacing of the equidistant grid, nData the length of the data input array, and shift is an offset of the samples to the symmetry axis and can usually be only 0 or 0.5 (input in units of stepSize).

Forward Abel Transform¶

The Forward Abel transform is defined as

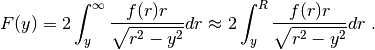
$F(y)=2\int_y^\infty\frac{f(r)r}{\sqrt{r^2-y^2}}dr\approx2\int_y^R\frac{f(r)r}{\sqrt{r^2-y^2}}dr\; .$

The Forward Abel Transform is chosen by setting forwardBackward=-1.

Backward (or Inverse) Abel Transform¶

The Backward (or Inverse) Abel transform is defined as

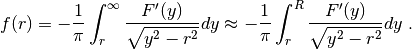
$f(r)=-\frac{1}{\pi}\int_r^\infty\frac{F'(y)}{\sqrt{y^2-r^2}}dy\approx-\frac{1}{\pi}\int_r^R\frac{F'(y)}{\sqrt{y^2-r^2}}dy\; .$

openAbel takes care of taking the derivate of the input data supplied by the user. The Backward Abel Transform is chosen by setting forwardBackward=1.

Backward (or Inverse) Abel Transform with Derivative Input¶

The Backward (or Inverse) Abel Transform with derivative input is defined as

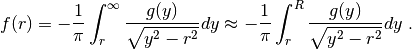
$f(r)=-\frac{1}{\pi}\int_r^\infty\frac{g(y)}{\sqrt{y^2-r^2}}dy\approx-\frac{1}{\pi}\int_r^R\frac{g(y)}{\sqrt{y^2-r^2}}dy\; .$

In contrast to the normal Backward Abel Transform, openAbel expects to get the derivative as input by the user.

The Backward Abel Transform with derivative input is chosen by setting forwardBackward=2.

Modified Forward Abel Transform¶

What we call the Modified Forward Abel Transform in openAbel is defined as the integral

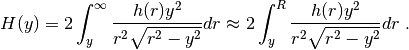
$H(y)=2\int_y^\infty\frac{h(r)y^2}{r^2\sqrt{r^2-y^2}}dr\approx2\int_y^R\frac{h(r)y^2}{r^2\sqrt{r^2-y^2}}dr\; .$

I encountered this integral when a radial electric field of an atom (which has a 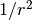$1/r^2$ singularity we want to integrate properly) is projected instead of a simpler function like with the normal Forward Abel Transform. One could just use the parameter shift = 0.5 instead to avoid the singularity of the electric field, but if one incorporates the singularity in the actual integral the convergence is much better. I recommend writing similar methods if one encounters other types of singularities in the Abel Transform.

The Modified Forward Abel Transform is chosen by setting forwardBackward=-2.